Table Of Content
Transformers play a vital role in electrical engineering by enabling efficient power transfer between circuits. Among various types of transformers, the concept of an ideal transformer serves as the foundation for understanding their operation. Although ideal transformers are theoretical models, they are essential for analyzing and designing practical systems. In this article, we will explore the basics of an ideal transformer, its characteristics, working principles, and how it differs from real-world transformers.
What is an Ideal Transformer?
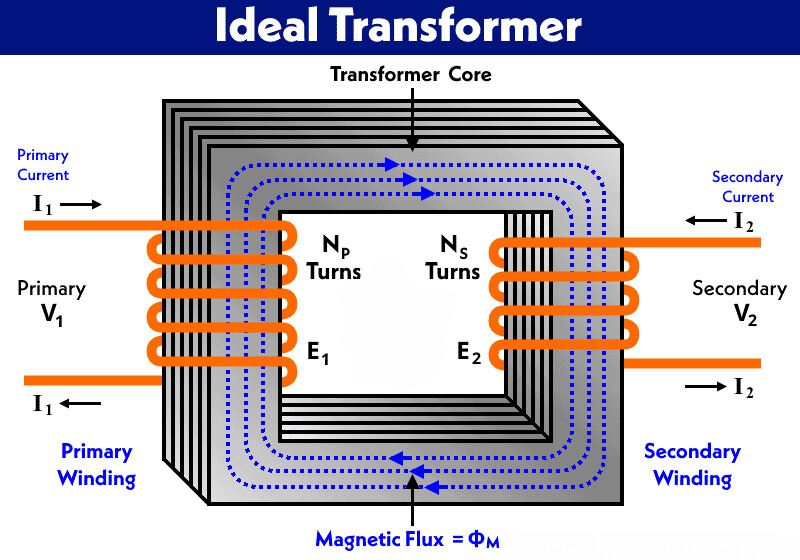
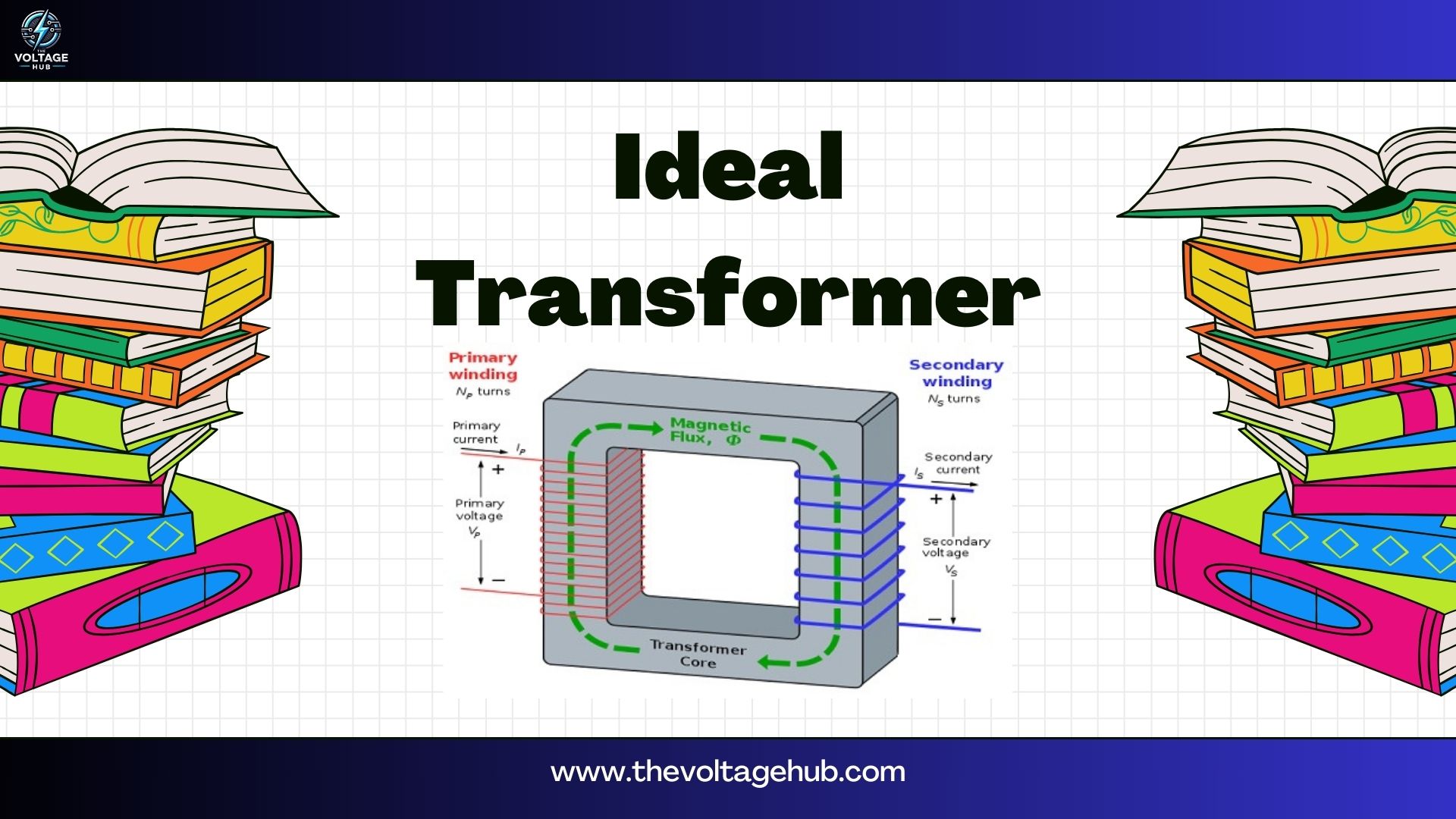
An ideal transformer is a hypothetical device that assumes perfect efficiency and operation. It simplifies transformer analysis by eliminating losses and imperfections. Key assumptions for an ideal X’mer include:
- No core losses: No energy is lost due to hysteresis or eddy currents.
- No winding resistance: The windings are perfect conductors.
- Perfect magnetic coupling: All magnetic flux links both primary and secondary windings.
- Infinite core permeability: The core requires no magnetizing current.
These assumptions make the ideal transformer an essential tool for studying and designing electrical systems.
How Does an Ideal Transformer Work?
The operation of an ideal transformer relies on Faraday’s Law of Electromagnetic Induction. When an alternating current (AC) flows through the primary winding, it generates a magnetic field in the core. This magnetic field induces a voltage in the secondary winding based on the following relationships:
- Voltage Transformation:
![]()
Here, V1 and V2 represent the primary and secondary voltages, while N1 and N2 are the number of turns in the respective windings.
- Current Transformation:
![]()
This relationship shows that the current in the windings adjusts inversely to the voltage ratio.
- Power Conservation:
An ideal transformer ensures no power is lost, making input power equal to output power.
Characteristics of an Ideal Transformer
Ideal transformers exhibit the following characteristics:
- High Efficiency: They transfer all input power to the output without losses.
- Accurate Voltage and Current Transformation: The output voltage and current precisely match the turns ratio.
- No Leakage Flux: All magnetic flux is confined to the core.
- Infinite Core Permeability: It eliminates the need for a magnetizing current.
These features make the ideal X’mer a simplified yet powerful model for understanding transformer behavior.
Applications of the Ideal Transformer Model
Although ideal transformers do not exist in real life, their model has significant applications:
- Simplifying Circuit Analysis: Engineers use the ideal X’mer model to analyze complex circuits.
- Studying Load Behavior: It helps predict how loads will react to voltage and current changes.
- Designing Practical Transformers: The model serves as a benchmark to compare real transformers and optimize their performance.
Differences Between Ideal and Practical Transformers
Understanding the differences between ideal and practical transformers is crucial:
| Feature | Ideal Transformer | Practical Transformer |
|---|---|---|
| Core Losses | Assumes no core losses (no hysteresis or eddy current losses). | Core losses occur due to hysteresis and eddy currents in the core. |
| Winding Resistance | Assumes zero resistance in the windings. | Windings have resistance, causing I²R losses. |
| Magnetic Coupling | Perfect magnetic coupling with no leakage flux. | Partial magnetic coupling; some leakage flux exists. |
| Efficiency | Operates at 100% efficiency. | Efficiency is less than 100% due to losses. |
| Power Transfer | Input power equals output power (no energy loss). | Input power is slightly greater than output power due to losses. |
| Core Permeability | Assumes infinite core permeability (no magnetizing current needed). | Finite core permeability; magnetizing current is required. |
| Complexity | Simple theoretical model for analysis and calculations. | Real-world model that requires complex calculations for accuracy. |
| Usage | Used for theoretical studies and simplifying transformer behavior | Used in practical applications with efficiency and design considerations. |
Limitations of the Ideal Transformer Concept
Despite its usefulness, the ideal transformer model has limitations. Its assumptions are unrealistic for practical applications. Real transformers experience losses, imperfect coupling, and efficiency drops. Over-reliance on this model can lead to inaccuracies when designing or analyzing real systems. Engineers must combine the ideal X’mer concept with practical considerations for accurate results.
Conclusion
The Ideal transformer is a powerful theoretical tool that simplifies the study of electrical systems. By assuming perfect efficiency and operation, it allows engineers to focus on fundamental principles without the complexities of real-world imperfections. While it’s essential to understand this model, practical transformer analysis is equally important for real-world applications.